前言

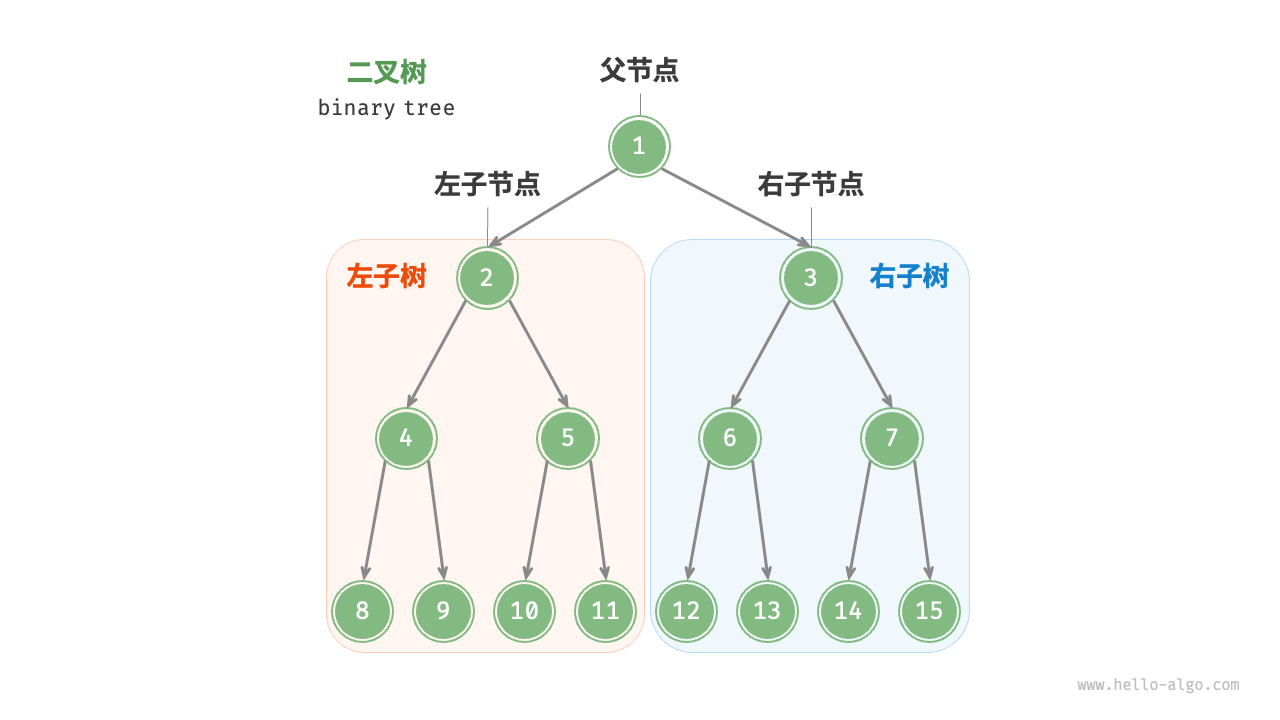
二叉树体现“一分为二”的逻辑。同链表相同，二叉树的最基本单位也是“节点”，节点包括节点值、左子节点引用、右子节点引用.节点的左子节点及其以下节点形成的树称为该节点的左子树（left subtree），同理可得右子树（right subtree）。

1.二叉树的一些属性

• 根节点：没有父节点的节点
• 叶节点：没有子节点的节点
• 二叉树的度：二叉树节点的子阶段数量，为0，1，或2
• 二叉树节点的层：根节点为1层，向下没经过一条边的节点的层级+1
• 二叉树的高度：根节点到最远叶节点之间的经过边的数量
• 二叉树节点的高度：在该节点所在子树上，距离该节点的最远叶节点之间的边数。

2.二叉树的基本操作

2.1 初始化二叉树

先构建根节点，然后创建指针引用

struct TreeNode{
    value:i32,
    leftNode:Option<Rc<RefCell<TreeNode>>>,
    RightNode:Option<Rc<RefCell<TreeNode>>>,
}
impl TreeNode{
    pub fn new（val:i32）-> Re<RefCell<Self>>{
		Rc::new(RefCell::new(
        	Self{
                val,
                leftNode:None,
                rightNode:None
            }
        ))
    }
}

fn main(){
    let n1 = TreeNode::new(1),
    let n2 = TreeNode::new(2),
    let n3 = TreeNode::new(3),
    let n4 = TreeNode::new(4),
    let n5 = TreeNode::new(5),
    
    n1.borrow_mut().leftNode = Some(n2.clone());
    n1.borrow_mut().rightNode = Some(n3);
    n2.borrow_mut().leftNode = Some(n4);
    n2.borrow_mut().rightNode = Some(n5);
}

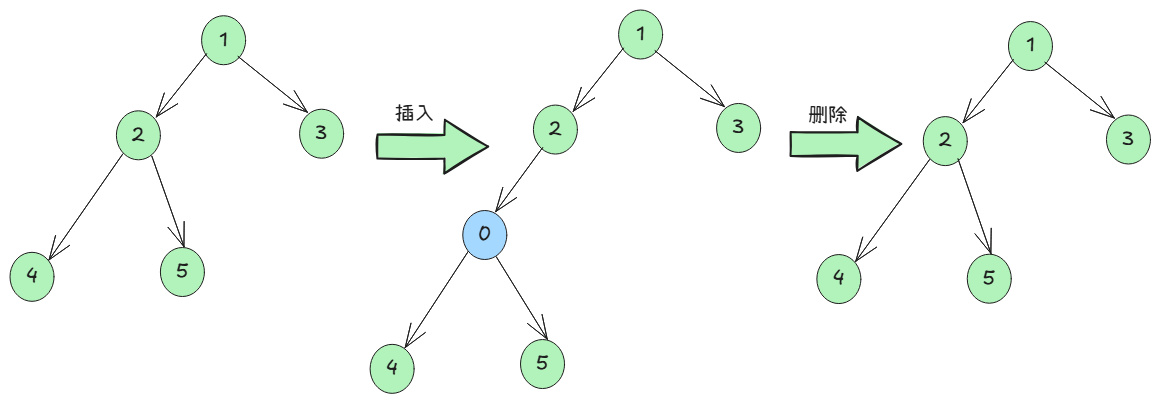
2.2 插入和删除二叉树节点

和链表插入、删除节点方法一致，改变树节点的指针指向即可，如在n2和n4，n5层之间插入节点n0：

let n0 = TreeNode::new(0);
n1.borrow_mut().leftNode = Some(n0.clone());
n0.brrow_mut().leftNode = Some(n2);

倘若再删除该节点，将n1的指针重新指向n2即可：

n1.brrow_mut().leftNode = some(n2)

初始、插入和删除示意图如下：

3. 常见二叉树的类型

3.1 完美二叉树

完美二叉树（perfect binary tree）的每一层的节点都被填充满，叶节点的度为0，其余所有节点的度均为2。完美二叉树又被称为“满树”。给定高度为h的二叉树，其节点树为：2^h+1 -1.

3.2 完全二叉树

完全二叉树(complete binary tree)仅允许最底层可以不被填满且由左向右递减。完美二叉树也是完全二叉树。

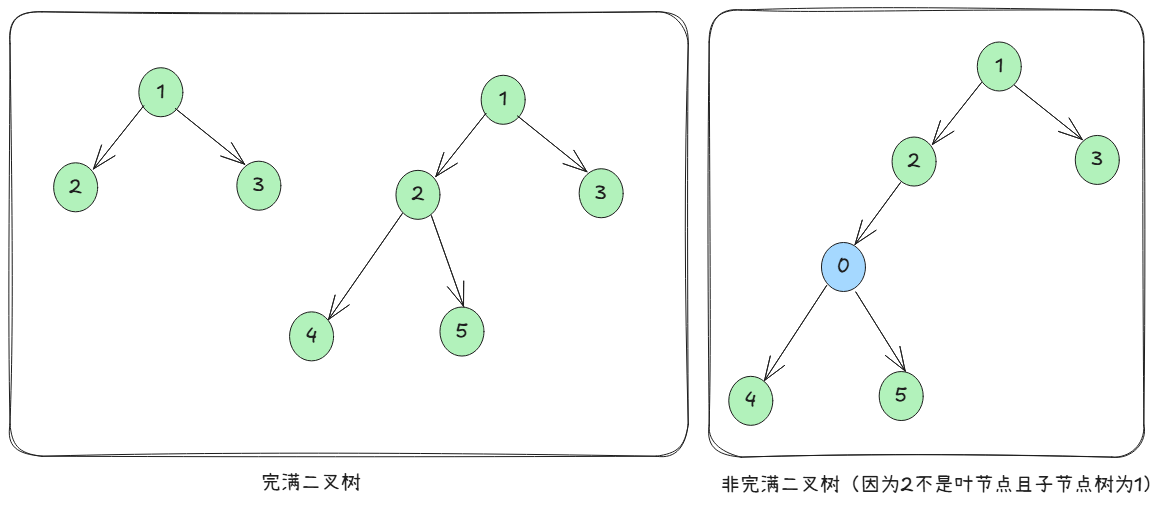
3.3 完满二叉树

完满二叉树（full binary tree）,除叶节点外，所有节点均有两个子节点。

3.4 平衡二叉树

平衡二叉树（balanced binary tree）的任意节点的左子树的高度和右子树的高度的差值的绝对值不超过1。